Направления исследований
- Волны в химических реакциях
- Динамика ансамблей связанных осцилляторов
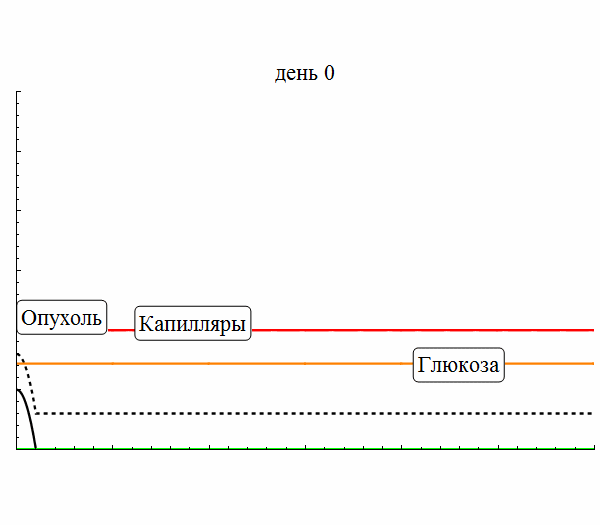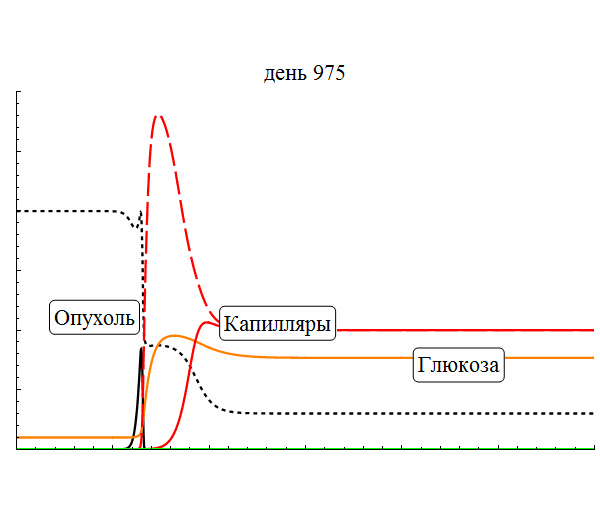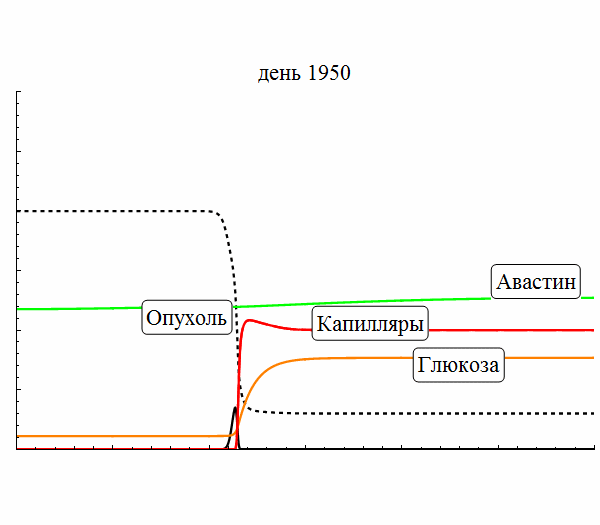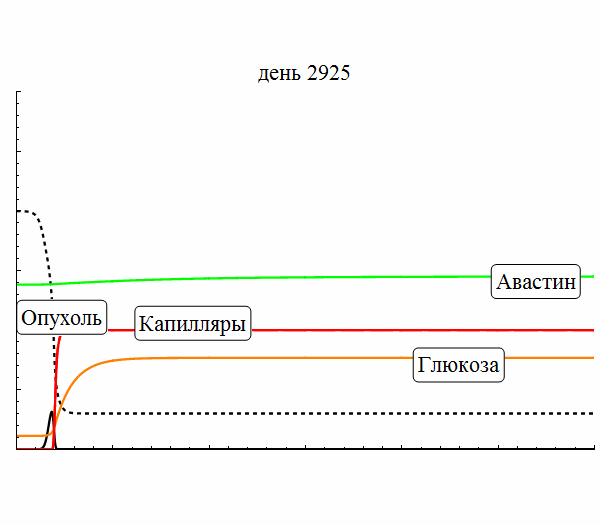
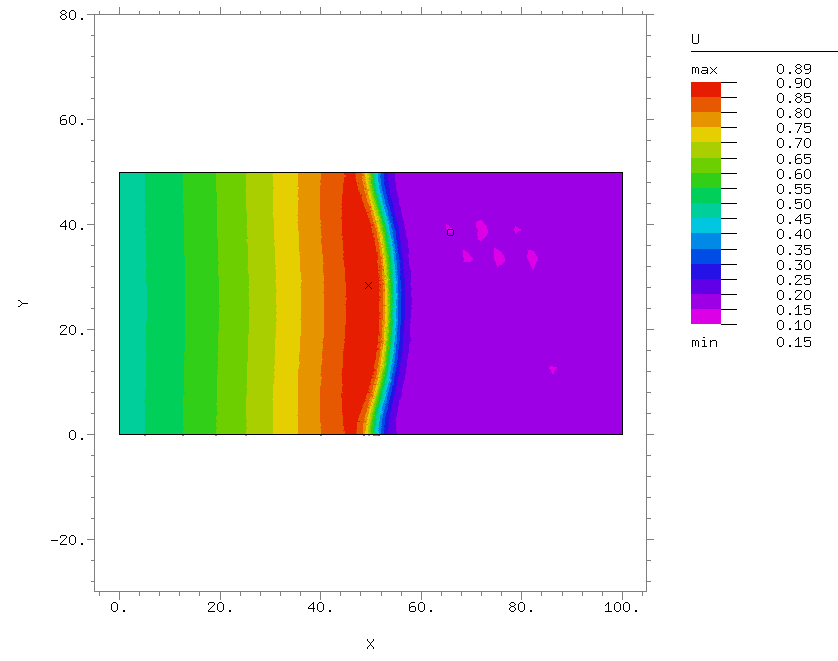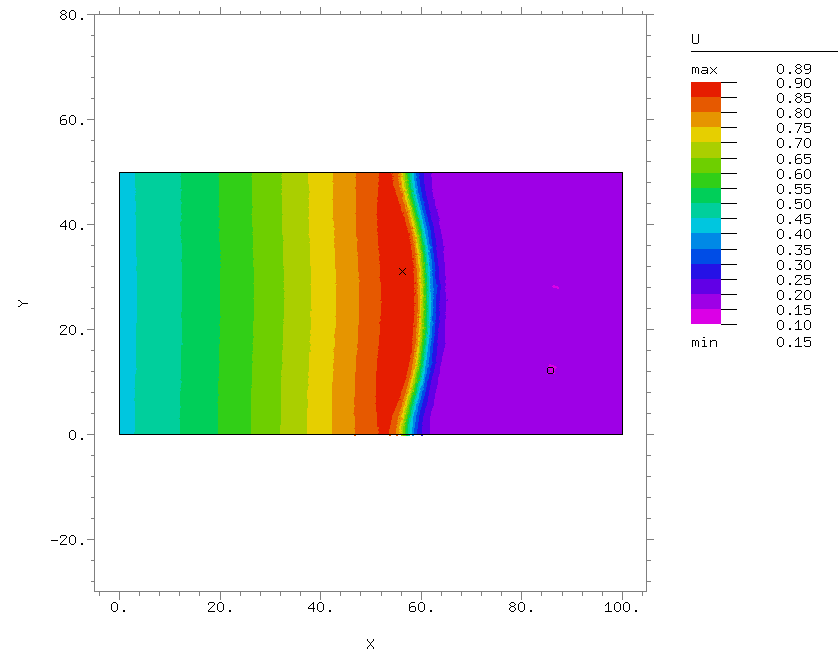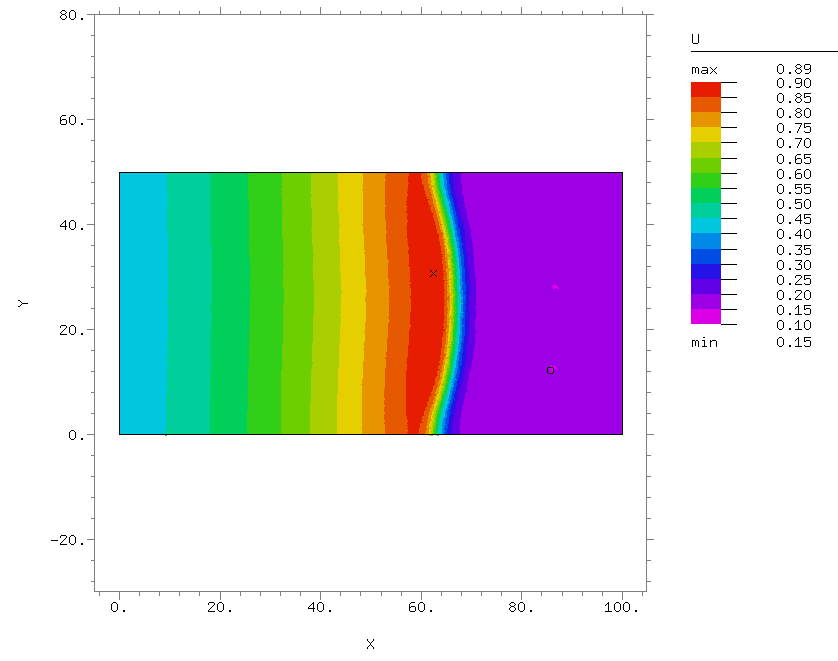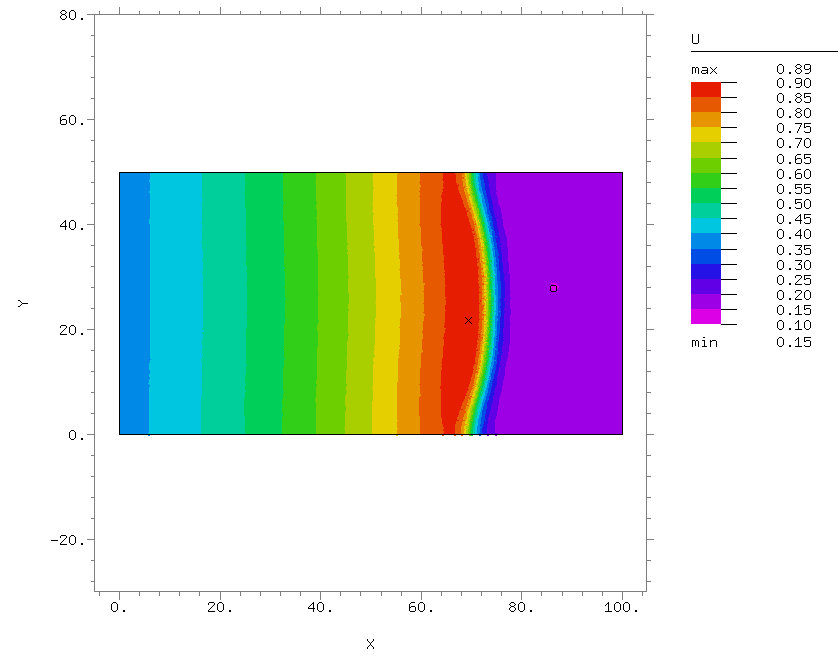
- Моделирование роста опухоли
- Динамика и структура волн горения
- Динамические режимы частичной синхронизации в нейросетях
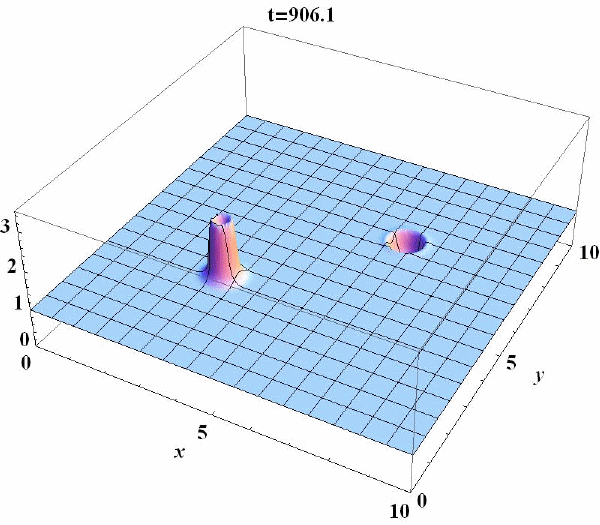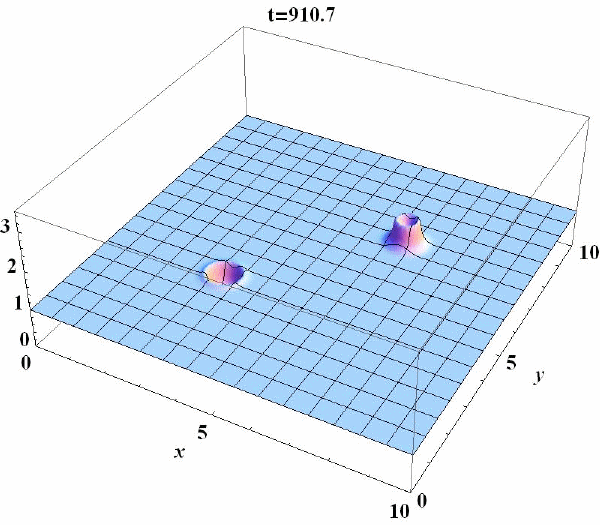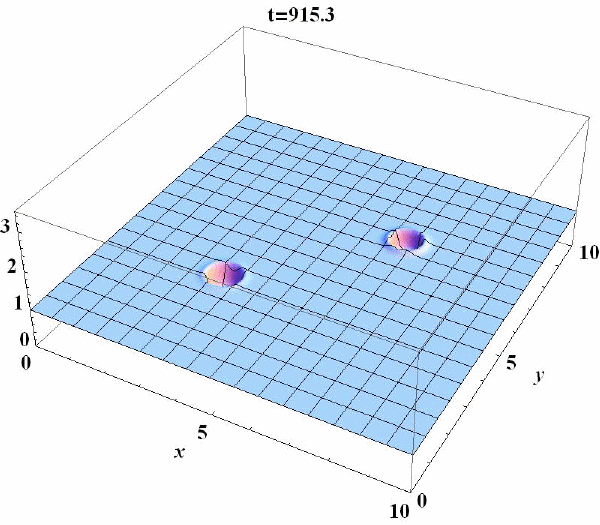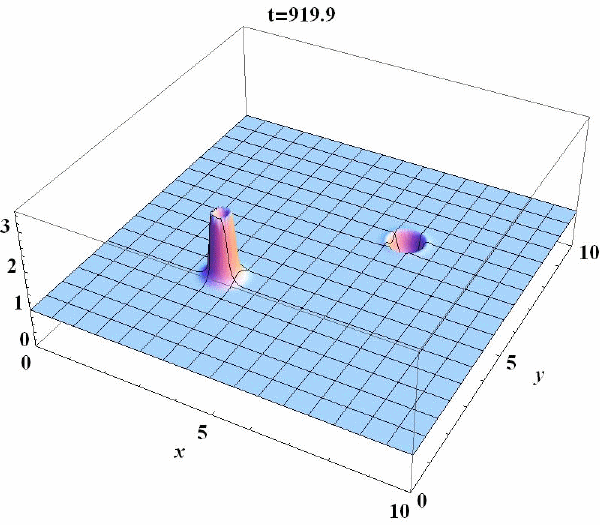
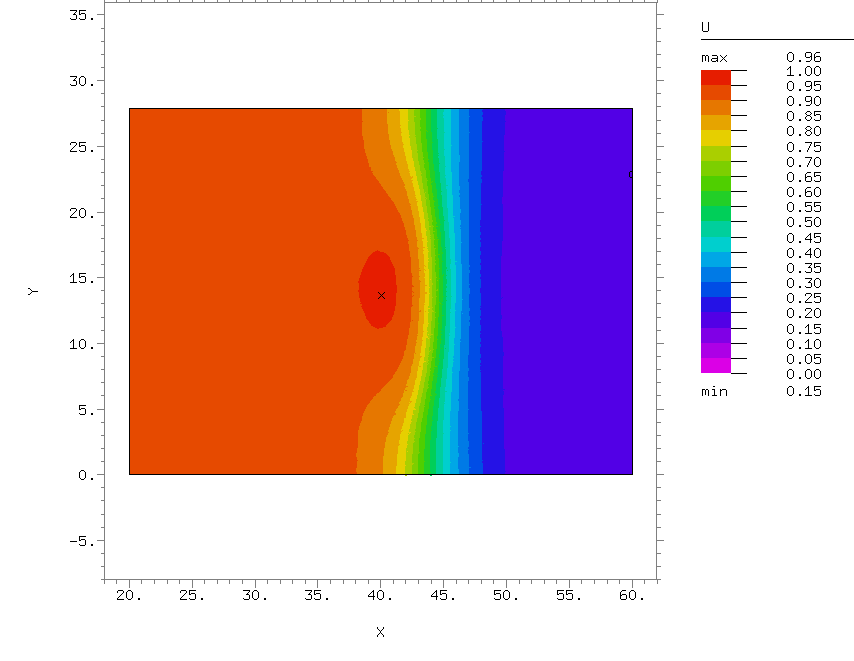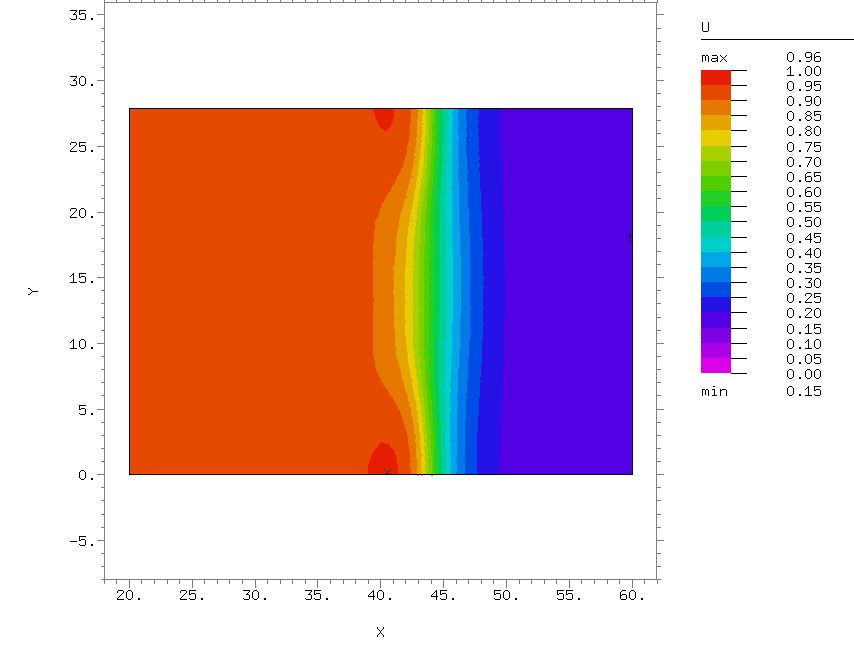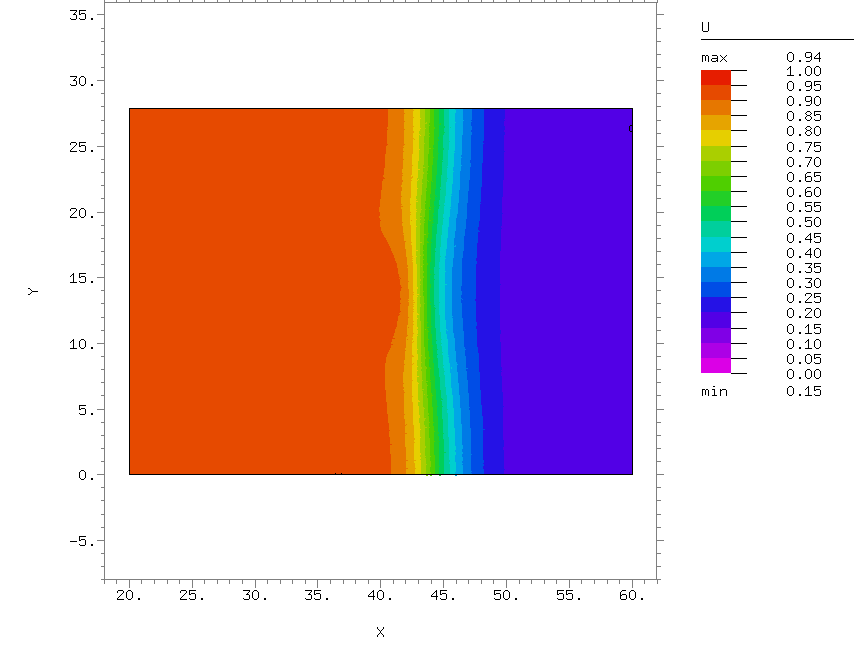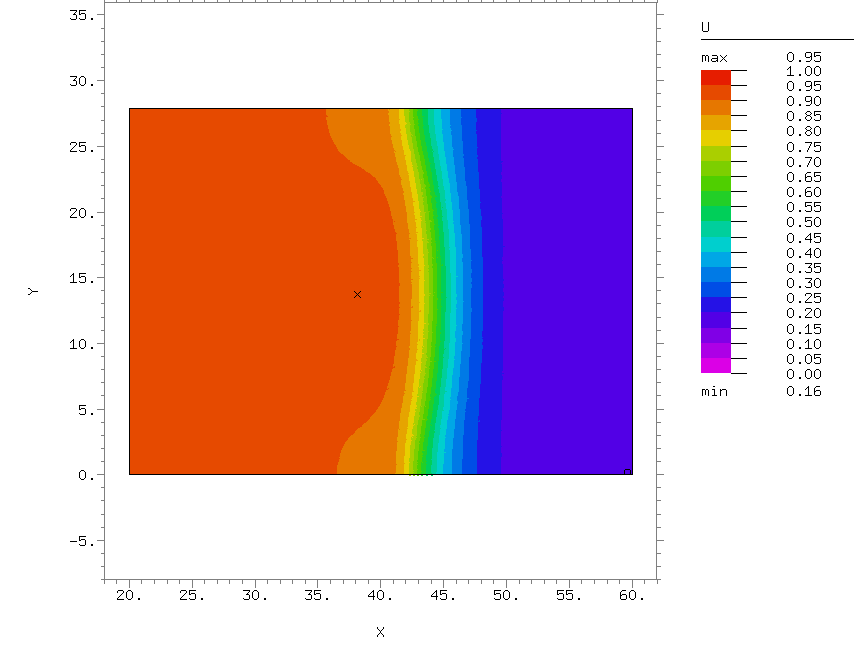
Механизмы пространственно-временной самоорганизации в химических системах
Явления самоорганизации, т.е. перехода системы в иное, как правило, более упорядоченное состояние, наблюдаются в системах различной природы: физических химических, биологических. Существенным свойством таких систем является то, что они открыты и далеки от состояния термодинамического равновесия. Именно это и является предпосылкой возникновения в них различных нетривиальных пространственно-временных режимов. Система может самоорганизоваться как во времени: например, она переходит из стационарного в колебательный режим, так и в пространстве: в частности, она может перейти из пространственно-однородного в неоднородное устойчивое состояние, или в ней могут возникнуть различные автоволновые режимы. Зачастую возникновение динамического хаоса также относят к явлениям самоорганизации.
По существу, вся деятельность нашей лаборатории лежит в русле изучений самоорганизации в различных системах. Вместе с тем, следует особо выделить направление, связанное с изучением пространственно-временной самоорганизации в химических системах. Это обусловлено тем, что, с одной стороны, к настоящему времени имеется ряд химических реакций, демонстрирующих в экспериментах сложное пространственно-временное поведение (ярким примером является реакция Белоусова- Жаботинского), а с другой, в силу их относительной простоты (по сравнению с биологическими системами) они допускают корректное изучение соответствующих механизмов самоорганизации с помощью математических моделей.
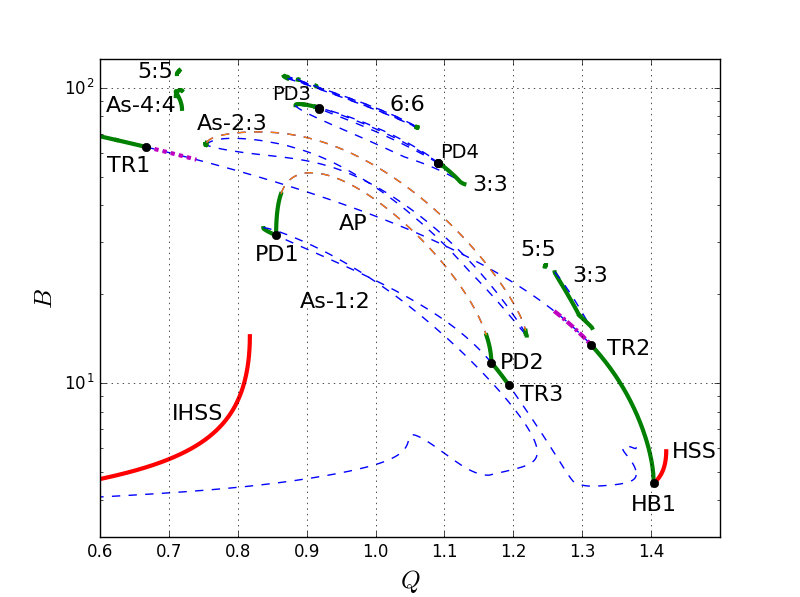
Конкретные задачи, которые решаются в рамках данного направления, – это изучение механизмов возникновения сложных пространственно-временных режимов, наблюдаемых в экспериментах с реакцией Белоусова-Жаботинского, протекающей, в частности, в водно-масляной микроэмульсии, а также механизмов возникновения структур на движущемся фронте реакции, например, на фронте волны горения.
Сотрудники
Губернов В.В. – д.ф.-м.н., ведущий научный сотрудник
Колобов А.В. – к.ф.-м.н., старший научный сотрудник
Полежаев А.А. – д.ф.-м.н., главный научный сотрудник, заведующий Лабораторией.
Фатеев И.С. – младший научный сотрудник.
Якупов Э.О. – младший научный сотрудник.
О нас
В 1972 году в Отделе теоретической физики ФИАН был образован Сектор проблем теоретической биофизики по инициативе возглавившего его Д.С. Чернавского и при поддержке руководителя ОТФ академика В.Л. Гинзбурга. Поначалу Сектор занимался исследованиями биологических систем, в частности, проблемой возникновения биологических ритмов, исследованием возможных механизмов биологического формообразования, механизмом переноса заряда в биологических макромолекулах, а также механизмом функционирования ферментов. В дальнейшем круг решаемых задач значительно расширился и вышел за пределы исключительно биологических. Был получен ряд важных результатов как общего характера, касающихся фундаментальных механизмов пространственно-временной самоорганизации в открытых неравновесных системах, так и относящихся к конкретным системам различной природы: физическим, химическим, биологическим.
В 2015 году Сектор был преобразован в Лабораторию нелинейной динамики и теоретической биофизики. Основное направление работы – исследование механизмов формирования пространственно-временных структур в нелинейных диссипативных динамических системах. В рамках этого направления решаются фундаментальные проблемы самоорганизации, а также разрабатывается математические модели, описывающие конкретные системы. В частности, в последнее время объектами теоретического исследования Лаборатории были сложные пространственно-временные режимы, экспериментально наблюдаемые в химических реакциях, таких как реакция Белоусова-Жаботинского, а также на распространяющемся фронте горения, рост и прогрессия злокачественной опухоли с учётом её взаимодействия с окружающими тканями и с кровеносными сосудами, сложные автоколебательные режимы, в том числе динамический хаос, в ансамблях связанных осцилляторов.
Последние публикации
- Chimera states in a lattice of superdiffusively coupled neurons, Chaos, Solitons & Fractals. – 2024. – Т. 181. – С. 114722. DOI: 10.1016/j.chaos.2024.114722
- Synchronization transitions in a system of superdiffusively coupled neurons: Interplay of chimeras, solitary states, and phase waves, Chaos: An Interdisciplinary Journal of Nonlinear Science. – 2024. – Т. 34. – №. 9. DOI: 10.1063/5.0226751
- Химерные состояния в системах супердиффузионно связанных нейронов, Известия Саратовского университета. Новая серия. Серия: Физика.– 2024. – Т. 24, – вып. 4. С. 328-339. DOI: 10.18500/1817-3020-2024-24-4-328-339, EDN: AKRGLX
- Evolutionary equations for the disturbed flame stabilised at the flat burner, S Minaev, E Sereshchenko, V Gubernov, Combustion Theory and Modelling, 1-18, 2024
- The performance of reaction mechanism in prediction of the characteristics of the diffusive-thermal oscillatory instability of methane–hydrogen–air burner-stabilized flames, A Moroshkina, E Yakupov, V Mislavskii, E Sereshchenko, A Polezhaev, S Minaev, V Gubernov, V Bykov, Acta Astronautica 215, 496-504, 2024
- Activation Energy of Hydrogen–Methane Mixtures, A Moroshkina, A Ponomareva, V Mislavskii, E Sereshchenko, V Gubernov, V. Bykov, S. Minaev, Fire 7 (2), 42, 2024
- Formation of spiral structures in rich-hydrogen air flames at elevated pressures, EO Yakupov, VV Gubernov, AA Polezhaev, International Journal of Hydrogen Energy 49, 784-795, 2024
- Relaxational oscillations of burner-stabilized premixed methane–air flames, D Volkov, A Moroshkina, V Mislavskii, E Sereshchenko, V Gubernov, V.Bykov, S.Minaev, Combustion and Flame 259, 113141, 2024
- Motion of magnetic motors across liquid–liquid interface, B Kichatov, A Korshunov, V Sudakov, V Gubernov, A Golubkov, A Kolobov, A Kiverin, L Chikishev, Journal of Colloid and Interface Science 652, 1456-1466, 2023
- Thermal Radiation Characteristics of Cylindrical Porous Burner with Axial Supply of Combustible Mixture, AD Moroshkina, AA Ponomareva, VV Mislavskii, EV Sereshchenko, VV Gubernov, SS Minaev, SN Tskhai, Bulletin of the Lebedev Physics Institute 50 (12), 515-520, 2023
- Determining the global activation energy of methane–air premixed flames, AD Moroshkina, AA Ponomareva, VV Mislavskii, EV Sereshchenko, VV Gubernov, VV Bykov, SS Minaev, Combustion Theory and Modelling 27 (7), 909-924, 2023
- Chimera states in a chain of superdiffusively coupled neurons, I.S. Fateev, A.A. Polezhaev, Chaos: An Interdisciplinary Journal of Nonlinear Science, v.33, 2023
- Influence of Heat Loss on the Chaotic Dynamics of Reaction Waves in the Model with Chain-Branching Reaction, M Kuznetsov, A Kolobov, V Gubernov, A Polezhaev, International Journal of Bifurcation and Chaos 33 (12), 2350137, 2023
- Dynamics of a chain of interacting neurons with nonlocal coupling, given by Laplace operator of fractional and variable orders with nonlinear Hindmarsh–Rose model functions, I.S. Fateev, A.A. Polezhaev, Bulletin of the Lebedev Physics Institute, v.50, p.243, 2023.
- Structure of Low Stretched Non-Premixed Counterflow Flames Stabilized in Planar Channel: Mass Spectrometric Study and Numerical Simulation, DA Knyazkov, TA Bolshova, RV Fursenko, ES Odintsov, AG Shmakov, VV Gubernov, SS Minaev, Combustion Science and Technology, 1-18, 2023
- Instability of Diverging Cylindrical Flame in Rotating Gas, SS Minaev, SN Mokrin, VV Gubernov, Bulletin of the Lebedev Physics Institute 50 (3), 91-96, 2023
- Experimental Study of Stretched Premixed Flame Stabilized in a Flat Channel near a Heated Wall, S Mokrin, V Gubernov, S Minaev, Metals 13 (2), 391, 2023
- Burner stabilized flames: Towards reliable experiments and modelling of transient combustion, A Moroshkina, V Mislavskii, B Kichatov, V Gubernov, V Bykov, U Maas, Fuel 332, 125754, 2023
- Pattern formation and collective effects during the process of the motion of magnetic nanomotors in narrow channels, B Kichatov, A Korshunov, V Sudakov, V Gubernov, A Golubkov, A Kiverin, Physical Chemistry Chemical Physics 25 (16), 11780-11788, 2023
СВЯЗЬ С НАМИ
Контакты
ФИАН, гл. здание, комн. 110-112Ленинский проспект, д.53, 19991 Москва. +7(499) 132-69-77, +7(499) 132-69-78
+7(499) 132-67-43 postmaster@lebedev.ru